NeuralODE

Neural ODE (astroNN.neuralODE; Neural Ordinary Differential Equation) module provides numerical integrator implemented in Tensorflow for solutions of an ODE system, and can calculate gradient.

Numerical Integrator

astroNN implemented numerical integrator in Tensorflow

astroNN.neuralode.odeint.odeint(func=None, x=None, t=None, aux=None, method='dop853', precision=tf.float32, *args, **kwargs)

To computes the numerical solution of a system of first order ordinary differential equations y’=f(x,y). Default precision at float32.

Parameters

• func (callable) – function of the differential equation, usually take func([position, velocity], time) and return velocity, acceleration

• x (Union([tf.Tensor, numpy.ndarray, list])) – initial x, usually is [position, velocity]

• t (Union([tf.Tensor, numpy.ndarray, list])) – set of times at which one wants the result

• method (str) – numerical integrator to use, available integrators are [‘dop853’, ‘rk4’]

• precision (type) – float precision, tf.float32 or tf.float64

• t – set of times at which one wants the result

Returns

integrated result

Return type

tf.Tensor

History

2020-May-31 - Written - Henry Leung (University of Toronto)

An example integration an ODE for sin(x)

import time
import pylab as plt
import numpy as np
import tensorflow as tf
from astroNN.shared.nn_tools import cpu_fallback, gpu_memory_manage
from astroNN.neuralode import odeint

cpu_fallback()
gpu_memory_manage()

# time array
t = tf.constant(np.linspace(0, 100, 10000))
# initial condition
true_y0 = tf.constant([0., 1.])
# analytical ODE system for sine wave [x, t] -> [v, a]
ode_func = lambda y, t: tf.stack([tf.cos(t), tf.sin(t)])

start_t = time.time()
true_y = odeint(ode_func, true_y0, t, method='dop853')
print(time.time() - start_t)  # approx. 4.3 seconds on i7-9750H GTX1650

# plot the solution and compare
plt.figure(dpi=300)
plt.title("sine(x)")
plt.plot(t, np.sin(t), label='Analytical')
plt.plot(t, true_y[:, 0], ls='--', label='astroNN odeint')
plt.legend(loc='best')
plt.xlabel("t")
plt.ylabel("y")
plt.show()

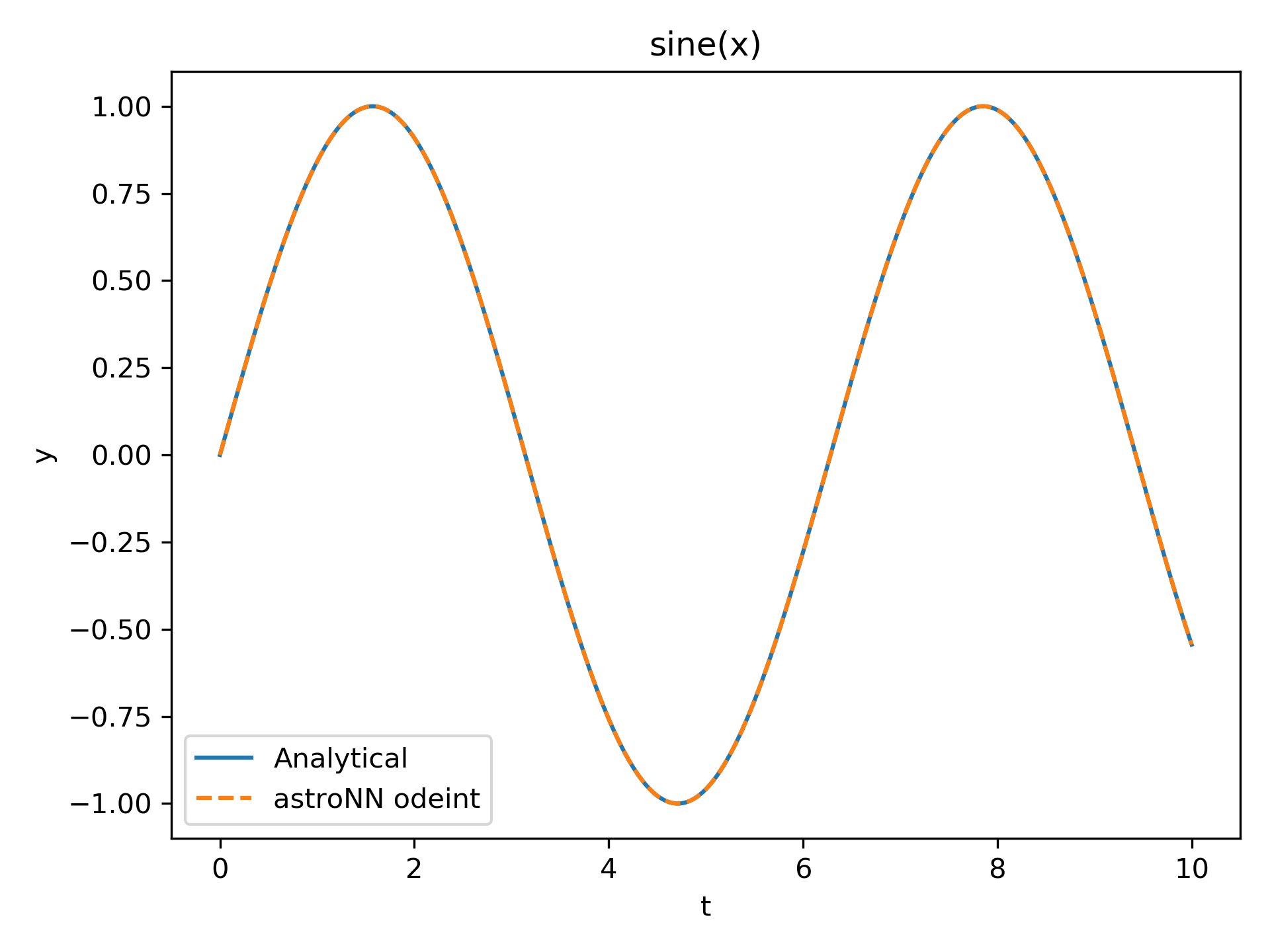
Moreover odeint supports numerically integration in parallel, the example below integration the sin(x) for 50 initial conditions. You can see the execution time is the same!!

start_t = time.time()
# initial conditions, 50 of them instead of a single initial condition
true_y0sss = tf.random.normal((50, 2), 0, 1)
# time array, 50 of them instead of the same time array for every initial condition
tsss = tf.random.normal((50, 10000), 0, 1)
true_y = odeint(ode_func, true_y0sss, tsss, method='dop853')
print(time.time() - start_t)  # also approx. 4.3 seconds on i7-9750H GTX1650

Neural Network model with Numerical Integrator

You can use odeint along with neural network model, below is an example

import numpy as np
import tensorflow as tf
from astroNN.shared.nn_tools import gpu_memory_manage, cpu_fallback
from astroNN.neuralode import odeint

cpu_fallback()
gpu_memory_manage()

t = tf.constant(np.linspace(0, 1, 20))
# initial condition
true_y0 = tf.constant([0., 1.])

class MyModel(tf.keras.Model):
    def __init__(self):
        super(MyModel, self).__init__()
        self.dense1 = tf.keras.layers.Dense(2, activation=tf.nn.relu)
        self.dense2 = tf.keras.layers.Dense(16, activation=tf.nn.relu)
        self.dense3 = tf.keras.layers.Dense(2)

    def call(self, inputs, t, *args):
        inputs = tf.expand_dims(inputs, axis=0)
        x = self.dense2(self.dense1(inputs))
        return tf.squeeze(self.dense3(x))

model = MyModel()

with tf.GradientTape() as g:
    g.watch(true_y0)
    y = odeint(model, true_y0, t)
# gradient of the result w.r.t. model's weights
g.gradient(y, model.trainable_variables)  # well define, no None, no inf or no NaN